1 Introduction

Advanced vehicle control features, including traction control, anti-lock braking systems, electronic stability control, adaptive cruise control, lane-keeping assistance, etc., have been topics of intense study over many years, and a variety of such functions have already been implemented to assist drivers. These and even more advanced driving automation functions are currently being readied for application to passenger cars, buses, and large vehicles whose handling requires superior driving skills. In particular, in emergency situations, advanced braking control is required to regulate the vertical vehicle control of vehicles of buses or trucks with large inertia and bring them to safe stops. Today, most buses and trucks are equipped with pneumatic braking systems that use compressed air as their energy medium. However, pneumatic braking systems have characteristics that make control design difficult [1,2,3,4]. First, large time delays occur due to the compressibility of air, and the dynamics of pneumatic braking systems inevitably mean that the relationship between the air medium and pressure flow is non-linear. Hence, when combined with the vehicle’s longitudinal dynamics, pneumatic braking systems are prone to various uncertainties. These include supply pressure variations due to brake application and release, temperature increases resulting from frequent braking, brake system component wear, vehicle load fluctuations, and changes in road surface conditions due to rain or snow.

Fig. 1
figure 1

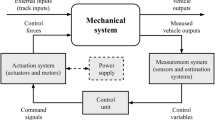
Overview of SMPC approach. SMPC explicitly describes the probabilistic uncertainties that need consideration when designing a robust control strategy using a probabilistic (also called chance) constraint. Here, \(\mathrm{{Pr}}({x} \le {x}^\mathrm{{max}}) \ge 1 - \alpha \), with \(\alpha \in (0, 0.5]\) is the allowable probability

Full size image

When considering such factors, model predictive control (MPC) [5], which considers dynamic coupling [6, 7], topographical information [8], and horizontal vehicle dynamics, provides an optimal control method for safe vehicle control during emergency stop conditions. For that reason, MPC is incorporated into a wide variety of automatic control systems such as train pneumatic braking systems [9], bus braking energy efficiency systems [10], and the steering systems of all-terrain cranes with slow dynamic response levels [11]. The high utility of MPC is its ability to solve the constrained optimization problem of a finite-time interval for each sampling step based on the model to be controlled. Then the controller applies the first component of the calculated input series in each sampling step. MPC makes it possible to calculate control inputs that explicitly consider functional, physical, and safety restrictions by applying constraints for input and state. However, MPC is vulnerable to the influence of actual motion factors that are not considered in models. Therefore, although preset constraints may be satisfied in MPC predictions, those constraints may be exceeded in actual conditions. MPC-based control has also been applied to heavy-duty commercial vehicle (HDCV) wheel slip control [12, 13], fuel consumption systems [14,15,16,17], automatic hydraulic transmission systems [18], actuator time delay controllers [19], pneumatic actuator controllers [20]. The challenge of the controller design of HDCVs are robustness against model uncertainty due to actuator or loading. The methods proposed in [21] is not considered against the uncertainty of the plant model. Also, the Kalman filer (KF) embedded MPC brake system [22] is available to use state covariance for the controller. To solve that, robust anti-slip control systems for different road surface environments [23] and systems that compensate for vehicle specification changes caused by load variations [24, 25] is reported. However, the deterministic constraints result in aggressive inputs when the model has stochastic uncertainty. This may result in the model not complying with the constraints as theory suggests.

In contrast, stochastic model predictive control (SMPC) is a robust control method that considers such uncertainties. In the SMPC approach, which is shown in Fig. 1, we can see that SMPC inputs a stochastic constraint called a “chance constraint” based on the probability distribution of the prediction error and designates it as the upper and lower limits of the state. This allows SMPC to explicitly describe the probabilistic uncertainties in designing the robust control strategy. For example, let the deterministic constraint be \(x \le x^\mathrm{{max}}\), with x as the states and \(x^\mathrm{{max}}\) as the upper limit states. If x is uncertain, the probability will not reach fifty percent. To avoid creating too large a value, the deterministic constraint needs to converted into a probabilistic (also called chance) constraint, in which \(\mathrm{{Pr}}({x} \le {x}^\mathrm{{max}}) \ge 1 - \alpha \), with \(\alpha \in (0, 0.5]\) is the allowable probability. In many applications, system uncertainties are often considered to be stochastic processes, which allows the incompleteness and uncertainties of set optimization problems to be taken into consideration. This suppresses erroneous control that can result from discrepancies between theory and an actual environment. SMPC can also improve both robustness and control performance using statistical information related to disturbances. For that reason, SMPC is also applied to uncertainties in automobile control [26,27,28]. On the other hand, external disturbances due to road environments, such as gradients and road surface friction coefficients, affect dynamic vehicle behaviors during emergency stops [22]. In such cases, wheel slip suppression improvements can be anticipated by considering the vehicle uncertainties, such as the brake pressure and road profile.

To facilitate this, this paper proposes a braking control method that considers the road profile outlined in Reference [29] as a stochastic uncertainty, and via which SMPC is applied to the control of HDCVs during emergency braking. The results of this study show that our proposed method improves braking system robustness against fluctuations in temperature, air brake system measurement values, and road surface features, all of which are mathematical programming problems involving random variables that are generally considered challenging to solve. In our method, we reformulate an SMPC into a deterministic equivalent model based on the expectations and covariances of random variables, which we achieve using the KF algorithm. This allows HDCV uncertainties to be controlled via the SMPC by considering disturbance-related statistical information. Hence, the primary contribution of this paper is the proposal of a braking control formulation that is robust against the probabilistic friction circle uncertainties affect. The remainder of this paper is organized as follows. The vehicle model, including an HDCV airbrake system, is described in Sect. 2, while road profiles are discussed in Sect. 3. Next, the KF-based state estimation is described in Sect. 4, while the SMPC-based controlled design is discussed in Sect. 5 and numerical simulation results are shown in Sect. 6. Finally, Sect. 7 concludes the paper.

Notations   This paper adopts the following notations. The subscripts \(\text{ fl }, \text{ fr }, \text{ rl },\) and \(\text{ rr }\) refer to front left, front right, rear left, and rear right, respectively. \(A := B\) refer to define A as B. \(N \sim {{\mathcal {N}}} (a, b)\) refer to the random variable N follows a normal distribution  \({{\mathcal {N}}} (a, b)\) with standard deviation a and variance b. \(\Vert {{\varvec{x}}}\Vert _{{\varvec{P}}} := \sqrt{{\varvec{x}}^\mathrm{T} {\varvec{P}} {\varvec{x}}}\) represents the weighted norm. \({\mathbb {R}}\) represents set of real numbers. Additionally, \({{\varvec{A}}} \succ {{\varvec{O}}}\), \({{\varvec{A}}} \succeq {{\varvec{O}}}\) denotes \({{\varvec{A}}}\) is a positive definite matrix and semi-positive definite matrix, respectively. \(\mathrm{{Pr}}(\cdot )\) represents probability, \({\mathbb {R}}^n\) represents an n-dimensional real vector, \({\mathbb {R}}^{n \times m}\) represents an \(n \times m\) real matrix, \({{\varvec{0}}}_n\) is n-dimensional zero vector, and \({{\varvec{O}}}_{n \times m}\) represents \(n \times m\) zero matrix. The subscript \(k+i \mid k\) refer to the predicted/estimated value of the variable for the time \(k+i\), which is given at time k.

2 Vehicle model

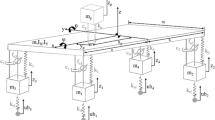
This section describes the equation of motion of HDCV’s kinematic and dynamic maneuvers in the horizontal X–Y plane, as shown in Fig. 2. To facilitate its adaptation as a control model, some assumptions are simplified.

Fig. 2
figure 2

3 DoF vehicle model with a reference path

Full size image

The vehicle kinematics model is expressed as follows:

$$\begin{aligned} \frac{ \mathrm {d} }{ \mathrm {d}t } \begin{bmatrix} X \\ Y \\ \psi \end{bmatrix} = \begin{bmatrix} V \cos (\beta + \psi ) \\ V \sin (\beta + \psi ) \\ \gamma \end{bmatrix}, \end{aligned}$$
(1)

where \(\gamma \) is the yaw rate, \(V = \sqrt{{v_x}^2 + {v_y}^2} \approx v_x\) is the vehicle velocity, \(\beta = \tan ^{-1} ({v_y}/{v_x}) \approx {v_y}/{v_x}\) is the vehicle side-slip angle, and \(v_x\) and \(v_y\) are, respectively, the longitudinal and lateral velocities in the vehicle frame. Let \(\beta ^{\mathrm {ref}} = 0\), reference vehicle kinematics is expressed as follows:

$$\begin{aligned} \frac{ \mathrm {d} }{ \mathrm {d}t } \begin{bmatrix} X^{\mathrm {ref}} \\ Y^{\mathrm {ref}} \\ \psi ^{\mathrm {ref}} \end{bmatrix}&= \begin{bmatrix} \cos \psi ^{\mathrm {ref}} \\ \sin \psi ^{\mathrm {ref}} \\ \rho ^{\mathrm {ref}} \end{bmatrix} V^{\mathrm {ref}}, \end{aligned}$$
(2)

where \(\rho ^{\mathrm {ref}}\) is road curvature. To incorporate lane-keeping, it is necessary to transform the lateral vehicle dynamics into path tracking error dynamics. In such cases, the relative errors between the ego and reference vehicles can be expressed as follows:

$$\begin{aligned} \begin{bmatrix} e_{x} \\ e_{y} \\ e_{\psi } \end{bmatrix}&= \begin{bmatrix} \cos \psi ^{\mathrm {ref}} &{} \sin \psi ^{\mathrm {ref}} &{} 0 \\ -\sin \psi ^{\mathrm {ref}} &{} \cos \psi ^{\mathrm {ref}} &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix} \begin{bmatrix} X - X^{\mathrm {ref}} \\ Y - Y^{\mathrm {ref}} \\ \psi + \beta - \psi ^{\mathrm {ref}} \end{bmatrix}. \end{aligned}$$
(3)

Next, assuming the vehicle side-slip angle \(\beta \) and the front-wheel steering angle \(\delta \) are small, the equations for the longitudinal, lateral, and yaw dynamics in the vehicle frame are expressed, respectively, as follows:

$$\begin{aligned}&{\dot{V}} = \dfrac{ F_{x \mathrm {fl}} + F_{x \mathrm {fr}} + F_{x \mathrm {rl}} + F_{x \mathrm {rr}}}{M}, \end{aligned}$$
(4a)
$$\begin{aligned}&{\dot{v}}_y = \dfrac{F_{y \mathrm {fl}} + F_{y \mathrm {fr}} + F_{y \mathrm {rl}} + F_{y \mathrm {rr}}}{M} - V \gamma , \end{aligned}$$
(4b)
$$\begin{aligned}&\begin{array}{ll} {\dot{\gamma }} =&{} \dfrac{(F_{y \mathrm {fl}} + F_{y \mathrm {fr}}) l_{\mathrm f} - (F_{y \mathrm {rl}} + F_{y \mathrm {rr}}) l_{\mathrm r}}{I_{z}} \\ &{} + \dfrac{(- F_{x \mathrm {fl}} + F_{x \mathrm {fr}}) w_{\mathrm f} + (- F_{x \mathrm {rl}} + F_{x \mathrm {rr}}) w_{\mathrm r}}{I_{z}}, \end{array}\end{aligned}$$
(4c)
$$\begin{aligned}&{\dot{s}}_\mathrm{{d}} = V, \end{aligned}$$
(4d)
$$\begin{aligned}&{\dot{\psi }} = \gamma , \end{aligned}$$
(4e)
$$\begin{aligned}&{\dot{e}}_{y} = v_y + V {e}_\psi , \end{aligned}$$
(4f)
$$\begin{aligned}&{\dot{e}}_{\psi } = \gamma - \rho ^{\mathrm {ref}} V, \end{aligned}$$
(4g)

where M is total vehicle mass, \(l_\mathrm{{f}}\) and \(l_\mathrm{{r}}\) are the distances from the center of gravity (CoG) to the front and rear axles, \(I_z\) is the vehicle body moment of inertia about the z-axis, and \(w_\mathrm{{f}}\) and \(w_\mathrm{{r}}\) are the widths of the front and rear track, respectively. In addition, \(F_{xij}\) and \(F_{yij}\) are the longitudinal and lateral tire forces, \(s_\mathrm{{d}}\) is the vehicle driving distance, and \({e}_{y}\) and \({e}_{\psi }\) denote the heading error and the lateral deviation values, respectively.

2.1 Longitudinal dynamics

When the slip ratio of each wheel is small (\(|{\lambda }|\ll 1\)), brake torque is approximated as follows:

$$\begin{aligned} T_{i}&\approx r_{\mathrm w} F_{xi}, \end{aligned}$$
(5)

where \(r_{\mathrm w}\) is the effective wheel rolling radius. Since this paper focuses on emergency vehicle stops, it deals solely with braking and does not consider driving-related aspects. We also assume that the pressure-braking force characteristics are linear, as outlined below:

$$\begin{aligned} F_{xi}&\approx -k_{\mathrm {b}} P_{i}, \end{aligned}$$
(6)

where \(k_{\mathrm {b}}\) is the proportional relationship constant of the brake pressure to the braking force characteristics. Since good mechanical lubrication is assumed, we ignore the effects of mechanical and viscous actuator friction. Hence, from (4), (5) and (6), the longitudinal dynamics can be expressed as follows:

$$\begin{aligned} \dot{{\varvec{x}}}_{\mathrm {lon}}&= {\varvec{A}}_{\mathrm {lon}} {\varvec{x}}_{\mathrm {lon}} + {\varvec{B}}_{\mathrm {lon}} {\varvec{u}}_{\mathrm {lon}}, \end{aligned}$$
(7)

with

$$\begin{aligned}&{\varvec{x}}_{\mathrm {lon}}= \begin{bmatrix} s_{\mathrm {d}}&V \end{bmatrix}^\mathrm{T}, ~~ {\varvec{u}}_{\mathrm {lon}} = \begin{bmatrix} P_{\mathrm {fl}}&P_{\mathrm {fr}}&P_{\mathrm {rl}}&P_{\mathrm {rr}} \end{bmatrix} ^\mathrm{T}, \\&{{\varvec{A}}}_{\mathrm {lon}} = \begin{bmatrix} 0 &{} 1 \\ 0 &{} 0 \\ \end{bmatrix}, ~~ {{\varvec{B}}}_{\mathrm {lon}} = \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 \\ \dfrac{-k_{\mathrm {b}}}{M} &{} \dfrac{-k_{\mathrm {b}}}{M} &{} \dfrac{-k_{\mathrm {b}}}{M} &{} \dfrac{-k_{\mathrm {b}}}{M} \end{bmatrix}. \end{aligned}$$
Fig. 3
figure 3

Air-brake system

Full size image

2.2 Lateral dynamics

Tire side-slip angles \(\alpha _i\) are expressed as follows [30, 31]:

$$\begin{aligned} \begin{aligned} \alpha _{\mathrm {fl, \, fr}}&= \tan ^{-1} \left( \frac{v_y + l_{\mathrm f} \gamma }{v_x \mp - w_{\mathrm f} \gamma /2} \right) - \delta , \\ \alpha _{\mathrm {rl, \, rr}}&= \tan ^{-1} \left( \frac{v_y - l_{\mathrm r} \gamma }{v_x \mp - w_{\mathrm r} \gamma /2} \right) , \end{aligned} \end{aligned}$$
(8)

where \(l_{\mathrm {f}}\) and \(l_{\mathrm {r}}\) are the CoG distances to the front and rear axle, respectively, and \(w_{\mathrm {f}}\) and \(w_{\mathrm {r}}\) are the front and rear track widths, respectively. Assuming \(|{\delta }|, |{\beta }|, |{\alpha _{\mathrm f}}|\), and \(|{\alpha _{\mathrm r}}|\ll 1\), \(\alpha _i\) is approximated as follows:

$$\begin{aligned} \begin{aligned} \alpha _{\mathrm f} = \alpha _{\mathrm {fl}} = \alpha _{\mathrm {fr}}&\approx \beta + \frac{l_{\mathrm f} \gamma }{V} - \delta , \\ \alpha _{\mathrm r} = \alpha _{\mathrm {rl}} = \alpha _{\mathrm {rr}}&\approx \beta - \frac{l_{\mathrm r} \gamma }{V}. \end{aligned} \end{aligned}$$
(9)

Next, assuming that the characteristics of the left and right tires are equal and that lateral tire forces \(F_{yi}\) are approximated as linear functions of the tire side-slip angles \(\alpha _i\), the lateral tire forces \(F_{yi}\) are approximated as follows:

$$\begin{aligned} \begin{aligned} F_{y{\mathrm f}}&= -2 K_{y{\mathrm f}} \alpha _{\mathrm f} = -2 K_{y{\mathrm f}} \Big ( \beta + \frac{l_{\mathrm f} \gamma }{V} - \delta \Big ), \\ F_{y{\mathrm f}}&= -2 K_{y{\mathrm r}} \alpha _{\mathrm r} = -2 K_{y{\mathrm r}} \Big ( \beta - \frac{l_{\mathrm r} \gamma }{V} \Big ), \end{aligned} \end{aligned}$$
(10)

where \(K_{y{\mathrm f}}\) and \(K_{y{\mathrm r}}\) are the cornering stiffness values. From (4) and (10), the lateral dynamics in the vehicle-fixed frame are expressed as follows:

$$\begin{aligned} \dot{{\varvec{x}}}_{\mathrm {lat}}&= {\varvec{A}}_{\mathrm {lat}} {\varvec{x}}_{\mathrm {lat}} + {\varvec{B}}_{\mathrm {lat}} u_{\mathrm {lat}} + {\varvec{E}}_{\mathrm {lat}} d + {\varvec{M}}_{\mathrm {lat}} {\varvec{u}}_{\mathrm {lon}} \end{aligned}$$
(11)

with

$$\begin{aligned}&{\varvec{x}}_{\mathrm {lat}} = \begin{bmatrix} e_{y}&{\dot{e}}_{y}&e_{\psi }&{\dot{e}}_{\psi } \end{bmatrix}^\mathrm{T}, ~~ {u}_{\mathrm {lat}} = \delta ,~~d = \rho ^\mathrm{{ref}}, \\&{{\varvec{A}}}_{\mathrm {lat}} = \begin{bmatrix} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} \dfrac{A_1}{V} &{} -A_1 &{} \dfrac{A_2}{V} \\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} \dfrac{A_3}{V} &{} -A_3 &{} \dfrac{A_4}{V} \\ \end{bmatrix},~~ {{\varvec{B}}}_{\mathrm {lat}} = \begin{bmatrix} 0 \\ B_1 \\ 0 \\ B_2 \\ \end{bmatrix}, \\&{{\varvec{M}}}_{\mathrm {lat}} = \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ - M_1 &{} M_1 &{} - M_2 &{} M_2 \end{bmatrix}, ~~ {{\varvec{E}}}_{\mathrm {lat}} = \begin{bmatrix} 0 \\ A_2 - V^2 \\ 0 \\ A_4 \\ \end{bmatrix}, \\&A_1 = -\dfrac{2}{M} (K_{y{\mathrm f}} + K_{y{\mathrm r}}), \\&A_2 = -\dfrac{2}{M} (l_{\mathrm f} K_{y{\mathrm f}} - l_{\mathrm r} K_{y{\mathrm r}}), \\&A_3 = -\dfrac{2}{I_z} (l_{\mathrm f} K_{y{\mathrm f}} - l_{\mathrm r} K_{y{\mathrm r}}), \\&A_4 = -\dfrac{2}{I_z} (l_{\mathrm f}^2 K_{y{\mathrm f}} + l_{\mathrm r}^2 K_{y{\mathrm r}}), \\&B_1 = \frac{2 K_{y{\mathrm f}}}{M}, ~~ B_2 = \frac{2 l_{\mathrm f} K_{y{\mathrm f}}}{I_z}, \\&M_1 = - \dfrac{k_{\mathrm {b}} w_{\mathrm {f}}}{2 I_z}, ~~ M_2 = - \dfrac{ k_{\mathrm {b}} w_{\mathrm {r}}}{2 I_z}. \end{aligned}$$

2.3 Air-brake model

The air-brake system structure is shown in Fig. 3. Assuming good mechanical lubrication, we ignore the effects of mechanical and viscous friction of actuators. This system consists of an air tank, a brake chamber, a solenoid, and a valve. The brake chamber is supplied with compressed air through the relay valve. We assume that the supply source is always filled with compressed air. The air pressure is adjusted by opening and closing the valve by the command voltage applied to the solenoid.

In this paper, we assume that a time delay occurs due to air propagation and that the time delay is modeled as a first-order delay system as follows:

$$\begin{aligned}&{P}_{i} = -\dfrac{1}{\tau _{i}} {P}_{i} + \dfrac{K_{i}}{\tau _{i}} {u}_{i},~{\forall i \in [{\mathrm {f}}, {\mathrm {r}}]}, \end{aligned}$$
(12)
$$\begin{aligned}&\dot{{\varvec{x}}}_{\mathrm {air}} = {\varvec{A}}_{\mathrm {air}} {\varvec{x}}_{\mathrm {air}} + {\varvec{B}}_{\mathrm {air}} {\varvec{u}}_{\mathrm {air}}, \end{aligned}$$
(13)

with

$$\begin{aligned} {\varvec{x}}_{\mathrm {air}}&= {\varvec{u}}_{\mathrm {lon}}, \, {\varvec{u}}_{\mathrm {air}} = \begin{bmatrix} u_{\mathrm {fl}}&u_{\mathrm {fr}}&u_{\mathrm {rl}}&u_{\mathrm {rr}} \end{bmatrix}^\mathrm{T}, \\ {{\varvec{A}}}_{\mathrm {air}}&= {\mathrm {diag}} \left\{ -\dfrac{K_{P{\mathrm {f}}}}{\tau _{\mathrm {f}}}, -\dfrac{K_{P{\mathrm {f}}}}{\tau _{\mathrm {f}}}, -\dfrac{K_{P{\mathrm {r}}}}{\tau _{\mathrm {r}}}, -\dfrac{K_{P{\mathrm {r}}}}{\tau _{\mathrm {r}}} \right\} , \\ {{\varvec{B}}}_{\mathrm {air}}&= {\mathrm {diag}} \left\{ -\dfrac{1}{\tau _{\mathrm {f}}}, -\dfrac{1}{\tau _{\mathrm {f}}}, -\dfrac{1}{\tau _{\mathrm {r}}}, -\dfrac{1}{\tau _{\mathrm {r}}} \right\} , \end{aligned}$$

where \(\tau _i\) and \(K_{Pi}\) are the time constant and gain of the air-brake system, respectively, which parameters are same as [21]. \(u_{i}\) is the command voltage, and \(P_{ij}\) is the brake pressure.

2.4 Vehicle load transfer

The formula used for the vehicle load transfer estimate is as follows [32]:

$$\begin{aligned} \begin{bmatrix} F_{z{\mathrm {fl}}} \\ F_{z{\mathrm {fr}}} \\ F_{z{\mathrm {rl}}} \\ F_{z{\mathrm {rr}}} \end{bmatrix}&= \begin{bmatrix} W_{\mathrm {f}} - W^{\mathrm {lon}} - W^{\mathrm {lat}}_{\mathrm {f}} \\ W_{\mathrm {f}} - W^{\mathrm {lon}} + W^{\mathrm {lat}}_{\mathrm {f}}\\ W_{\mathrm {r}} + W^{\mathrm {lon}} - W^{\mathrm {lat}}_{\mathrm {r}}\\ W_{\mathrm {r}} + W^{\mathrm {lon}} + W^{\mathrm {lat}}_{\mathrm {r}} \end{bmatrix}, \end{aligned}$$
(14)

with

$$\begin{aligned}&W_{\mathrm {f}} = \Big ( \dfrac{ m_{\mathrm {s}} l_{\mathrm {r}}}{l} + m_{\mathrm {suf}} \Big ) \dfrac{\mathrm{g}}{2}, \\&W_{\mathrm {r}} = \Big ( \dfrac{ m_{\mathrm {s}} l_{\mathrm {f}}}{l} + m_{\mathrm {sur}} \Big ) \dfrac{\mathrm{g}}{2}, \\&W^{\mathrm {lon}} = \dfrac{ m_{\mathrm {s}} h_{\mathrm {g}} a_x}{2 l}, \\&W^{\mathrm {lat}}_i = \dfrac{ m_{\mathrm {s}} h_{\mathrm {g}} a_y}{2 w_{i}},~~\forall i \in [{\mathrm {f}},{\mathrm {r}}], \end{aligned}$$

where \(L=l_\mathrm{f}+l_\mathrm{r}\) is the wheelbase, \(m_\mathrm{s}\) is the vehicle sprung mass, \(m_{\mathrm {uf}}\) and \(m_{\mathrm {ur}}\) are the vehicle front and rear spring mass, respectively, \(\mathrm{g}\) is the acceleration due to gravity, \(h_\mathrm{g}\) is the CoG height, and \(r_w\) is the effective tire rolling radius.

2.5 State equation

From (4), (7), (11) and (13), the augmented systems of longitudinal, lateral, and air-brake model are expressed as follows:

$$\begin{aligned} \dot{{\varvec{x}}}&= {\varvec{A}} {\varvec{x}} + {\varvec{B}} {\varvec{u}} + {\varvec{E}} d \end{aligned}$$
(15)

with

$$\begin{aligned} {\varvec{x}}&= \begin{bmatrix} {{\varvec{x}}}_{\mathrm {lon}}^\mathrm{T}&{{\varvec{x}}}_{\mathrm {lat}}^\mathrm{T}&{{\varvec{x}}}_{\mathrm {air}}^\mathrm{T} \end{bmatrix}^\mathrm{T} \in {\mathbb {R}}^{10}, \\ {\varvec{u}}&= \begin{bmatrix} {{\varvec{u}}}_{\mathrm {air}}^\mathrm{T}&{u}_{\mathrm {lat}} \end{bmatrix} ^\mathrm{T} \in {\mathbb {R}}^{5}, \\ {{\varvec{A}}}&= \begin{bmatrix} {{\varvec{A}}}^{\mathrm {lon}} &{}&{} ~{\varvec{O}}_{2 \times 4} &{} ~{{\varvec{B}}}^{\mathrm {lon}} \\ {\varvec{O}}_{4 \times 2} &{} &{}~{{\varvec{A}}}^{\mathrm {lat}} &{} ~{\varvec{M}}_{\mathrm {lat}} \\ &{}{{\varvec{O}}_{4 \times 6}} &{}&{} ~{{\varvec{A}}}^{\mathrm {air}} \end{bmatrix}\in {\mathbb {R}}^{10 \times 10}, \\ {{\varvec{B}}}&= \begin{bmatrix} &{}{{\varvec{O}}_{2 \times 5}} &{}\\ {\varvec{O}}_{4 \times 4} &{}&{} ~{{\varvec{B}}}^{\mathrm {lat}} \\ {{\varvec{B}}}^{\mathrm {air}} &{}&{} ~{\varvec{0}}_{4} &{} \\ \end{bmatrix} \in {\mathbb {R}}^{10 \times 5}, \\ {{\varvec{E}}}&= \begin{bmatrix} {\varvec{0}}_{2} \\ {\varvec{E}}^{\mathrm {lat}} \\ {\varvec{0}}_{4} \\ \end{bmatrix} \in {\mathbb {R}}^{5}. \end{aligned}$$
Table 1 k values of ISO-8608 road roughness classification
Full size table

3 Road profile

Because there is such a wide variety of road surface environments, including asphalt, cobblestones, and unpaved ground, the International Organization for Standardization (ISO) has classified road surface conditions into eight levels (from A to H) in the ISO 8608 [33] standard. This standard also classifies road surface height \(z_\mathrm{g}(s_\mathrm{{d}})\), which is expressed as follows:

$$\begin{aligned} z_\mathrm{g}(s_\mathrm{{d}})&= \textstyle \sum \limits _{i = 1}^{\infty } A_n \{ S (f_n) \} \cos {(2 \pi f_n s_\mathrm{{d}} + \theta _n)} \end{aligned}$$
(16)

with

$$\begin{aligned} S (f_n) = S (f_0) \left( {\dfrac{f_n}{f_0}} \right) ^{-2}, ~~ S (f_0) = (2^k \cdot 10^{-3})^2, \end{aligned}$$

where \(A_n\) is the complex Fourier coefficient, \(f_0 = 1/ (2 \pi )\), and \(f_n\) is the spatial frequency, \(S(f_n)\) is the power spectral density (PSD) function, and \(\theta \sim {\mathcal {U}}(0, 2 \pi )\) is the phase with a uniform distribution. We consider the finite partial sum up to the N term for the infinite series of (16) [34].

First, from the Fourier spectrum, \({\varPsi }(f_n)\) of \(S(f_n)\) is defined as follows:

$$\begin{aligned} S (f_n)&:= \lim _{\Delta f \rightarrow 0} {\dfrac{|{\varPsi ^2}|}{\Delta f}} = \lim _{\Delta f \rightarrow 0} {\dfrac{\varPsi \cdot \varPsi ^{*}}{\Delta f}}, \end{aligned}$$
(17)

where \(\varPsi ^{*}\) is the conjugate complex number of \(\varPsi \), and the Fourier spectrum \({\varPsi }\) is the effective value of the complex Fourier coefficient \(A_n\), i.e., \(\varPsi = {A_n}/\sqrt{2}\). Accordingly, if we let \(L_{\mathrm{road}}\) be the overall road length and assume the bandwidth is \(f_n \approx n \Delta f = 2 \pi /L_{\mathrm{road}}\), \(S(f_n)\) can be approximated as follows:

$$\begin{aligned} S (f_n)&\approx {\dfrac{\varPsi ^2}{\Delta f}} = {\dfrac{A_n^2}{2 \Delta f}}. \end{aligned}$$
(18)

Then, we substitute (18) into (16), the finite sum up to the N term can be expressed as follows:

$$\begin{aligned} z_\mathrm{g}(s_\mathrm{{d}})&= \textstyle \sum \limits _{i = 1}^{N} \varGamma \sqrt{\Delta f} \left( {\dfrac{f_n}{f_0}} \right) \cos {(2 \pi i \Delta f s_\mathrm{{d}} + \theta _n)}, \end{aligned}$$
(19)

where \(\varGamma =2^k \cdot 10^{-3}\), \(s_\mathrm{{d}} \in [0, L_\mathrm{road}]\), \(\Delta f = 1/L_\mathrm{road}\), \(n^\mathrm{{max}} = 1/f^\mathrm{{max}}\), \(N = n^\mathrm{{max}}/{\Delta n} = L_{\mathrm{road}}/f^\mathrm{{max}}\), and \(f^\mathrm{{max}}\) is the highest spatial frequency. The road surface unevenness degree is expressed by the k value of \(S(f_0)\). The correspondence between the k values and the eight road state classifications are listed in Table 1. The A and B classes correspond approximately to asphalt, while the D–E classes correspond to irregular roads. The road profile (with respect to the driving distance represented by (16)) is shown in Fig. 4, where \(L_{\mathrm{road}} = 250\) m, and \(N = 2500\). Increased k values indicate increased vertical height.

Fig. 4
figure 4

ISO-8608 road surface profiles

Full size image
Fig. 5
figure 5

Q–Q plot of road profile (D–E class)

Full size image
Fig. 6
figure 6

Histogram of road profile (D–E class)

Full size image

Next, we will examine the distribution of road profile characteristics. The D–E class road profile histogram is shown in Fig. 6. To compare similarities between normal and sample distributions, the quantile–quantile (Q–Q) plot of the D–E class road profile is shown in Fig. 5 where the horizontal axis is the quantiles of the standard normal distribution, and the vertical axis is the sample quantiles. As the quantiles increase in similarity, the tendency of the blue dots to follow the straight line indicated by the red alternating long-short dashed line increases. The green line shows the interquartile. As can be seen in Fig. 5, the road profile characteristics differ from the normal distribution.

4 Kalman filter

In this paper, the output is expressed as follows:

$$\begin{aligned} {{\varvec{y}}} = {{\varvec{C}}} {{\varvec{x}}} = \begin{bmatrix} s_\mathrm{{d}}&e_{y}&e_{\psi }&P_{\mathrm {fl}}&P_{\mathrm {fr}}&P_{\mathrm {rl}}&P_{\mathrm {rr}} \end{bmatrix} ^\mathrm{T}, \end{aligned}$$
(20)

and the unobtainable state is estimated by KF. First, the estimation model discretized (15) by the zero-order hold at the sampling time \(\Delta t\) is expressed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{\varvec{x}}}_{k + 1} = {\varvec{A}}_\mathrm{{d}} {{\varvec{x}}}_{k} + {\varvec{B}}_\mathrm{{d}} {{\varvec{u}}}_{k} + {\varvec{E}}_\mathrm{{d}} {d}_{k} + {\varvec{w}}_{k}, \\&{\varvec{y}}_{k} = {\varvec{C}} {\varvec{x}}_{k} + {\varvec{v}}_{k}, \end{aligned}\right. \end{aligned}$$
(21)

where \({\varvec{A}}_\mathrm{{d}}, {\varvec{B}}_\mathrm{{d}},\) and \({\varvec{E}}_\mathrm{{d}}\) collectively define the coefficient matrix of a discrete-time system, \({\varvec{w}} \sim {{\mathcal {N}}} ({{\varvec{0}}}, {{\varvec{\Sigma }}}_{{\varvec{w}}})\) and \({\varvec{v}} \sim {{\mathcal {N}}} ({{\varvec{0}}}, {{\varvec{\Sigma }}}_{{\varvec{v}}})\) are the process and observation noises, respectively, and \({{\varvec{\Sigma }}}_{{\varvec{w}}} \succeq {{\varvec{O}}}\) and \({{\varvec{\Sigma }}}_{{\varvec{v}}} \succ {{\varvec{O}}}\) are the covariance of the process and observation noises, respectively. Then, the prediction steps are calculated as

$$\begin{aligned} {\hat{{\varvec{x}}}}_{k \mid k - 1}&= {{\varvec{A}}}_\mathrm{{d}} \hat{{\varvec{x}}}_{k - 1 \mid k - 1} + {{\varvec{B}}}_\mathrm{{d}} {{\varvec{u}}}_{k - 1} + {{\varvec{E}}}_\mathrm{{d}} {d}_{k - 1}, \end{aligned}$$
(22a)
$$\begin{aligned} {{\varvec{P}}}_{k \mid k - 1}&= {{\varvec{A}}}_\mathrm{{d}} {\varvec{P}}_{k - 1 \mid k - 1} {{\varvec{A}}}_\mathrm{{d}}^\mathrm{T} + {\varvec{\Sigma }}_{{\varvec{w}}}, \end{aligned}$$
(22b)

where \({\hat{{\varvec{x}}}}_{k \mid k - 1}\) and \({{\varvec{P}}}_{k \mid k - 1}\) are the a priori state estimate and error covariance, respectively. The filtering steps are calculated as

$$\begin{aligned} {\varvec{M}}_{k}&= {{\varvec{P}}}_{k \mid k - 1} {\varvec{C}}^\mathrm{T} ({\varvec{C}} {{\varvec{P}}}_{k \mid k - 1} {\varvec{C}}^\mathrm{T} + {\varvec{\Sigma }}_{{\varvec{v}}} )^{-1}, \end{aligned}$$
(23a)
$$\begin{aligned} {\hat{{\varvec{x}}}}_{k \mid k}&= {{\varvec{A}}}_\mathrm{{d}} \hat{{\varvec{x}}}_{k \mid k-1} + {\varvec{M}}_{k} ({\varvec{y}}_{k} - {{\varvec{C}}} \hat{{\varvec{x}}}_{k \mid k-1} ), \end{aligned}$$
(23b)
$$\begin{aligned} {{\varvec{P}}}_{k \mid k}&= ({\varvec{I}} - {{\varvec{M}}_{k}} {{\varvec{C}}} ) {{\varvec{P}}}_{k \mid k - 1}, \end{aligned}$$
(23c)

where \({\varvec{M}}_{k}\) is the Kalman gain, and \({\hat{{\varvec{x}}}}_{k \mid k}\) and \({{\varvec{P}}}_{k \mid k}\) are the a posteriori state estimate and error covariance, respectively.

5 Stochastic MPC-based vehicle control

This section describes the formulation of the optimization problem designed to achieve vehicle stability. First, we describe the cost function required to balance the input and state priority necessary to achieve the desired performance, after which we describe the constraints. In particular, we examine how uncertainty is considered via the chance constraint in the optimization problem.

5.1 Cost function

In this paper, the evaluation function of the following equation is defined as follows:

$$\begin{aligned} J =&\Vert {\tilde{{\varvec{x}}}_{k + H \mid k}}\Vert _{{{\varvec{Q}}}_{\mathrm f}}^2 + \textstyle \sum \limits _{i=0}^{H - 1} ( \Vert {\tilde{{\varvec{x}}}_{k + i \mid k}}\Vert _{{\varvec{Q}}}^2 + \Vert {{{\varvec{u}}}_{k + i \mid k}}\Vert _{{{\varvec{R}}}_{{\varvec{u}}}}^2 \nonumber \\&+ \Vert \Delta {{\varvec{u}}}_{k + i \mid k}\Vert _{{{\varvec{R}}}_{{\varvec{\Delta u}}}}^2 ) + \Vert {\varepsilon }_{k} \Vert ^2_{\rho _{\varepsilon }}, \end{aligned}$$
(24)

where \({{{\varvec{u}}}_{k}}\) is the current time input, \({\Delta {{\varvec{u}}}_k} = {{\varvec{u}}}_k - {{\varvec{u}}}_{k-1} \), \({\tilde{{\varvec{x}}}_k} = {\hat{{\varvec{x}}}_k}-{{{\varvec{x}} }^{\mathrm {ref}}_k} \) is the error between the estimated state \({\hat{{\varvec{x}}}_k}\) at the current time and the target state \({{{\varvec{x}}}^{\mathrm {ref}}_k}\), \({{\varvec{Q}}} ~\succeq {{\varvec{O}}} \) is the stage cost weight matrix, \({{\varvec{R}}} ~\succ {{\varvec{O}}}\) is the input weight matrix, \({{\varvec{Q}}}_{\mathrm f}\succeq {{\varvec{O}}}\) is the terminal cost weight matrix, and H is a horizon. Additionally, \(\rho _\varepsilon \) is a weight constant for the slack variable \(\varepsilon \).

5.2 Constraints

By designing a brake pressure \(P_{i}\) constraint that satisfies the friction circle \(\sqrt{F_{xi}^2 + F_{yi}^2} \le \mu _{i} F_{zi}\), vehicle slip occurrence is suppressed. Here, \(\mu _{i}\) and \(F_{zi}\) are the road surface friction coefficient and vertical force, respectively. From the relational expression of the circle of forces and (6), the limit value of the brake pressure \(P_{i}\) is expressed by the following inequality:

$$\begin{aligned} 0&\le P_{i} \le \dfrac{1}{k_{\mathrm {b}}} \sqrt{(\mu _i F_{zi})^2 - F_{yi}^2},\ {\forall i \in [{\mathrm {fl}}, {\mathrm {fr}}, {\mathrm {rl}}, {\mathrm {rr}}]}. \end{aligned}$$
(25)

In addition, the speed constraint for not taking into account backward movement, the upper and lower limits for the command voltage of the air brake system, and the lateral deviation \(e_y\) constraint for preventing lane departure are set as follows:

$$\begin{aligned} V&> 0, \end{aligned}$$
(26)
$$\begin{aligned} u_{i}^\mathrm{{min}}&\le u_{i} \le u_{i}^\mathrm{{max}},\ {\forall i \in [{\mathrm {fl}}, {\mathrm {fr}}, {\mathrm {rl}}, {\mathrm {rr}}]}, \end{aligned}$$
(27)
$$\begin{aligned} - e_y^\mathrm{{max}}&\le e_y \le e_y^\mathrm{{max}}. \end{aligned}$$
(28)
Fig. 7
figure 7

SMPC system Block diagram

Full size image

Next, we will explain how to transform the chance constraint into a deterministic constraint to solve the stochastic optimization problem as an equivalent deterministic problem [35]. First, let \({\varvec{g}}_{j}\) be a jth basis vector, and let the jth component of the state be given by  \(x_{j}={{\varvec{g}}_{j}^\mathrm{T} {\varvec{x}}_{k}}\). Then, the chance constraint of \(x_{j}\) is

$$\begin{aligned} \mathrm{{Pr}} ({x}_{j} \le {x}^\mathrm{{max}}_{j} ) \ge 1 - \alpha _{j}, \end{aligned}$$
(29)

where \( \eta _{j} := 1 - \alpha _j\) and \(\alpha _j\) is allowable probability. Since we focus solely on design brake pressure chance constant here, \(\alpha _{j}\) is expressed as follows:

$$\begin{aligned} \alpha _{j}&= {\left\{ \begin{array}{ll} 1/2, &{} \forall j \in \{1, \cdots , 6\}, \\ \alpha , &{} \forall j \in \{7, \cdots , 10\}. \end{array}\right. } \end{aligned}$$
(30)

Note that \(\alpha = 1/2\) is equivalent to the deterministic constraint. As can be seen in Fig. 6, the road profile is an asymmetrical and multimodal distribution, so an approximation as a Gaussian distribution is not reasonable. Therefore, from the Chebyshev–Cantelli inequality [36], the expected value \(\mathrm {E}({\varvec{x}}_k) = {\hat{{\varvec{x}}}}_{k \mid k}\), and the variance \(\sigma _{j}^2={\varvec{g}}_{j}^\mathrm{T} {{\varvec{P}}}_{k \mid k} {\varvec{g}}_{j}\), the chance constraint is transformed as follows:

$$\begin{aligned} {\hat{x}}_{j}&\le x^\mathrm{{max}}_{j} - x^\mathrm{{margin}}_{j}, \end{aligned}$$
(31)

where \(x^\mathrm{{margin}}_{j} := \sqrt{ \zeta {\varvec{g}}_{j}^\mathrm{T} {{\varvec{P}}}_{k \mid k} {\varvec{g}}_{j}}\), \(\zeta = {\eta _{j}}/{(1 - \eta _{j})}\). Even though it is a conservative constraint, it is possible to use the Chebyshev–Cantelli inequality to deal with general distributions.

5.3 Optimization problem

Using a vehicle model, a cost function, and the relevant constraints, a deterministic equivalent constrained stochastic programming is expressed as follows:

Deterministic equivalent SMPC:

$$\begin{aligned} \begin{array}{c@{~~}l} \min \limits _{[\Delta {{\varvec{U}}}^\mathrm{T} \varepsilon ]^\mathrm{T}} &{} (24) \\ \text {w.r.t.} &{} {{\varvec{u}}}_{k + l \mid k}, {\forall l \in [0, H - 1]} \\ \text {s.t.} &{} {{\varvec{x}}}(0) = {{\varvec{x}}}_0, \\ &{}\begin{array}{ll} \hat{{\varvec{x}}}_{k + l + 1 \mid k}=&{} {\varvec{A}}_\mathrm{{d}} \hat{{\varvec{x}}}_{k + l \mid k} + {\varvec{B}}_\mathrm{{d}} {{\varvec{u}}}_{k + l \mid k}\\ &{}+ {\varvec{E}}_\mathrm{{d}} {d}_{k + l \mid k}, \end{array} \\ &{}\underline{\hat{{\varvec{x}}}}_{k} + \hat{{\varvec{x}}}^\mathrm{{margin}} \le \hat{{\varvec{x}}}_{k + i + 1 \mid k} \le \overline{\hat{{\varvec{x}}}}_{k} - \hat{{\varvec{x}}}^\mathrm{{margin}}, \\ &{}\underline{{\varvec{u}}}_{k} \le {\varvec{u}}_{k + i \mid k} \le \overline{{\varvec{u}}}_{k}, \\ &{}\varepsilon \ge {0}, \end{array} \end{aligned}$$

where \(\Delta {\varvec{U}} = [\Delta {{\varvec{u}}}_{k \mid k}^\mathrm{T}\,\Delta {{\varvec{u}}}_{k + 1 \mid k}^\mathrm{T}\,\cdots \,\Delta {{\varvec{u}}}_{k + H -1 \mid k}^\mathrm{T}]^\mathrm{T}\), \(\underline{{\varvec{\bullet }}} \) \(:= {{\varvec{\bullet }}}^\mathrm{{min}} - \varepsilon {\varvec{v}}^\mathrm{{min}}_{{\varvec{\bullet }},\mathrm {ECR}}\) , \(\overline{{\varvec{\bullet }}} := {{\varvec{\bullet }}}^\mathrm{{max}} + \varepsilon {\varvec{v}}^\mathrm{{max}}_{{\varvec{\bullet }}, \mathrm {ECR}}\).

To avoid infeasibility, the state and input constraints are relaxed by the slack variable [37]. The relaxation degree is adjusted by Equal Concern for Relaxation (ECR) \({\varvec{v}}^\mathrm{{max}}_{{\varvec{\bullet }}, \mathrm {ECR}}\). Note that \({\varvec{v}}^\mathrm{{max}}_{{\varvec{\bullet }}, \mathrm {ECR}} = 0\) refers to a hard constraint that is relaxed as the value of the ECR increases.

6 Simulation result and discussion

The control system is shown in Fig. 7. Here, it can be seen that KF estimates the state acquired from the controlled object. The SMPC control input is calculated using the target value, a measurable disturbance, and the estimated value. The control target is a four-axle eight-wheel TruckSim truck model provided by Virtual Mechanics. In this study, we used the default Magic Formula (MF) model in TrcuckSim as our tire model. We also considered it difficult to identify the MF parameters from time to time due to the various changes in road conditions. Therefore, in our control model for MPC, we assume that the tire force is linear for the longitudinal and lateral slip of the tire as mentioned in Sects. 2.1 and 2.2. In SMPC, this is considered to be a two-axle four-wheel vehicle model with \(l_\mathrm{{f}} = (l_1 + l_2)/2, l_\mathrm{{r}} = (l_3 + l_4)/2\), where \(l_i\) is the distance from the front to the i th axle and the CoG. The truck model inputs are the brake torque \(T_i\) and the handle angle \(\delta _\mathrm{{SW}}\). The brake torque is calculated by (5) and distributed to each axle as \(T_{1,2} = T_\mathrm{{f}}/2, T_{3,4} = T_\mathrm{{r}}/2\). The steering wheel angle \(\delta _\mathrm{{SW}}\) is calculated by \(\delta _\mathrm{{SW}} = n_\mathrm{{gear}} \delta \), where \(n_\mathrm{{gear}}\) is the steering gear ratio. The vehicle specifications used in the equation of state are listed in Table 2, while the SMPC control parameters are listed in Table 3 and the estimated KF parameters are as shown in Table 4. Chance constraints are designed for each of the four-wheel brake pressures, each of which had the same allowable probability \(\alpha \). In this study, the value of the speed weights is set to a large value to stop the vehicle quickly. In this way, the weights are designed to emphasize tracking to the target speed. In the driving scenario shown in Fig. 8, the road surface is a split-\(\mu \) circular route with \(\mu \) on the left and right sides in the direction of travel set at 0.6 and 0.9, respectively, and be known in this study. This road surface information is assumed to be known. The turning radius of the circular path is r = 152.4 m. Assuming emergency braking conditions, the target speed \({V}^{\mathrm {ref}}\) is changed from 70 km/h to 0 km/h at time 2. Additionally, the target state is \({\varvec{x}}^\mathrm{{ref}}=[({\varvec{x}}^\mathrm{{ref}}_\mathrm{{lon}})^\mathrm{T}~({\varvec{x}}^\mathrm{{ref}}_\mathrm{{lon}})^\mathrm{T}~({\varvec{x}}^\mathrm{{ref}}_\mathrm{{lon}})^\mathrm{T}]^\mathrm{T}\), where \({\varvec{x}}^\mathrm{{ref}}_\mathrm{{lon}} = [s_{\mathrm {d}}^\mathrm{{ref}}~V^\mathrm{{ref}}]^\mathrm{T}\), \(s_{\mathrm {d}} = \int V^{\mathrm {ref}} \mathrm{d}t\), \({\varvec{x}}^\mathrm{{ref}}_\mathrm{{lat}} = {{\varvec{0}}}_4^\mathrm{T}\), \({\varvec{x}}^\mathrm{{ref}}_\mathrm{{air}} = {{\varvec{0}}}_4^\mathrm{T}\). Hence, the left and right road surfaces are different, and the longitudinal and lateral force act at the same time. The control performance validity in this scenario is verified through emergency braking. Note that the brake pressure noise follows a normal distribution of \({\mathcal {N}}(0, \sigma _\mathrm{{f,r}}^2)\). In this study, braking performance verification is conducted on roads with uneven surfaces, as shown in the D–E class of Fig. 4 and be unknown in this study. The MPC results are also shown for comparison purposes. The SMPC/MPC iteration max is set to 50.

Table 2 Vehicle parameters
Full size table
Table 3 Control parameters
Full size table
Table 4 Estimate parameters
Full size table
Fig. 8
figure 8

Simulation scenario involving a braking turn on a split-\(\mu \) road

Full size image
Fig. 9
figure 9

Comparison between SMPC and MPC during braking on a split-\(\mu \) road with aa vertical road profile displacement broken down by a trajectory, b longitudinal speed of the vehicle CoG, c lateral deviation, and d quadratic programming (QP) iterations. e Traveling distance. f Key Performance Indicators (KPIs) The red and blue solid lines show the SMPC and MPC cases, respectively, while the green dashed line shows the reference trajectory and the chain lines show constraints. The yellow line shows that using QP is infeasible, while the chain line shows the max iterations

Full size image
Fig. 10
figure 10

Execution time. a SMPC (fixed with \(\Delta t = 100\) ms). b MPC (fixed with \(\Delta t = 100\) ms). c SMPC (fixed with \(H_\mathrm{p} = 10\)). d MPC (fixed with \(H_\mathrm{p} = 10\))

Full size image

In this figure, the black-filled area shows the time evolution after the vehicle has stopped. A comparison between SMPC and MPC model results during braking on a split-\(\mu \) road with a vertical road profile displacement is shown in Fig. 9. The red and blue solid lines show the cases of SMPC and MPC, respectively. The green dashed line shows the reference trajectory. Trajectories on the X–Y plane are shown in Fig. 9a, while Fig. 9b shows the time evolution of the vehicle longitudinal speed. The lateral deviation time evolution is shown in Fig. 9c. The chain line shows constraints. The time evolution of QP iterations is shown in Fig. 9d. Here, the yellow line shows that using the QP is infeasible, while the chain line shows max iterations. The time evolution of traveling distance is shown in Fig. 9e. The Key Performance Indicators (KPIs) is shown in Table 5 and Fig. 9f, where index factor is max deceleration, max corrective steering angle, max traveling distance, mean front wheels slip ratio, mean rear wheels slip ratio, max yaw rate [13]. The time evolution of execution time is shown in Fig. 10, while Fig. 10a, c and Fig. 10b, d show the SMPC and MPC cases, respectively. The time evolution of brake pressure in the SMPC case is shown in Fig. 11, while Fig. 11a and b show the SMPC and MPC cases, respectively. Additionally, the slip ratio of each wheel in the SMPC case are shown in Fig. 12, while Fig. 12a shows the slip ratio of first and second axle wheels. Next, Fig. 12b shows the slip ratio of third and fourth axle wheels, while Fig. 13 shows the slip ratio of each wheel in the MPC case.

Table 5 KPIs
Full size table
Fig. 11
figure 11

Brake pressure of the front left wheel during braking on the split-\(\mu \) road with vertical road profile displacement. The green marker shows the measurement values while the red solid line shows the estimation. The blue solid line shows the upper bound predicted by the tire friction circle, while the yellow solid line shows the true value. The violet dashed line shows 2\(\sigma \) confidence interval: a SMPC. b MPC

Full size image
Fig. 12
figure 12

Slip ratio during braking in a turn on an split-\(\mu \) road (SMPC). The blackfilled area shows the time evolution after the vehicle has stopped. a First and second left/right wheels, b third and fourth left/right wheels

Full size image
Fig. 13
figure 13

Slip ratio during braking in a turn on an split-\(\mu \) road (MPC). The black-filled area shows the time evolution after the vehicle has stopped. a First and second left/right wheels, b third and fourth left/right wheels

Full size image

The vehicle braked while maintaining lane tracking in each case, as shown in Fig. 9a. As shown in Fig. 9c, the lateral deviation constraint was violated in both the SMPC and MPC cases because it was necessary to allow the slack variable constraint to be violated to make the chance constraint of the friction circle feasible. In addition, the lateral deviation in the SMPC case was smaller than in the MPC case because the solution became infeasible in the MPC case when its optimality was lost at the 2-s mark, as shown in Fig. 9d. Hence, when considering the statistical information related to disturbances, the results of this study show that lane followability and running stability during braking on a split-\(\mu \) circular route are improved by the use of SMPC. In Fig. 9b, we can see that the SMPC simulation stopping time was slightly longer than the MPC stopping time. However, As shown in Fig. 9e, stopping distance of SMPC is 71.8 m and MPC is 72.2 m. Also, as shown Table 5 and in Fig. 9f, SMPC KPIs are improved compared with MPC KPIs. The slip ratio during braking in the SMPC case, as shown in Fig. 12, was smaller than the MPC case, as shown in Fig. 13. This is because SMPC considers the confidence interval of the brake pressure to be a chance constraint and is more conservative than the original constraint, as shown in (31) and Fig. 11. As a result, slippage due to uncertainty is suppressed, as shown in Fig. 12. In the MPC case, the brake pressure uncertainty is not explicitly considered, so the ratio of time exceeding the tire friction circle constraint is higher than that of SMPC, which means the vehicle slipped more, as shown in Fig. 13. The slip ratio values in the black-filled area oscillated after the vehicle stopped as shown in Figs. 12 and 13. This is because the formula for calculating the vehicle skid angle has a term that includes velocity in the denominator, and the calculation becomes unstable due to division by zero as the vehicle is braked. From Fig.10, the longer the prediction horizon \(H_\mathrm{p}\) is, the more dimensionality of the matrices handled in the optimization calculation. Therefore, the average and peak execution times are longer. In all cases of \(H_\mathrm{p} = 10, 7, 5\), the computation time peaked at 2 s, which is the start of stopping, but it was below the sampling time of MPC \(\Delta t = 100\) ms. This is because the vehicle switched from constant driving, which does not reach the friction circle constraint, to braking, which does reach the friction circle constraint. As a result, the active constraints in the effective constraint method were updated, and the Hesse matrix of the Lagrangian function was re-evaluated. This resulted in a temporary increase in the run time by 2 s.

7 Conclusions

This paper proposed a method of SMPC that considers the uncertainty of brake pressure and road profiles in relation to the emergency braking of heavy-duty commercial vehicles (HDCVs). Herein, the proposed method was verified through a simulation involving turning braking on a split-\(\mu \) road. The running stability of an HDCV ensured stable conditions in areas where the controlling braking force and the lateral force interacted.